これまでは、ブログに書いてから、Wordデータにしていたけど、Wordからそのままコピペしたほうが早いことに気づいた。図も綺麗に載るんだね…知らなかったよ。
さて、抄読会で担当になった部分が追加になったので、資料を下のように準備した。
資料
10月 -こういうときには死亡率を使えばいいんですね-
[前提]
割合(propotion): 割合とは全体のなかで特定の特徴をもつものが閉める部分の大きさを言う。たとえば、集団のなかでの喫煙者の割合など。
割合=a/(a+b)
比(ratio): 比とは、異なるもの同士を割り算で比較したものである。たとえば、ある疾病が男に多いのか女に多いのかを示す場合に、性比(男の患者数/女の患者数)を用いることがある。
比=a/b
性比の場合には、a、bともに含まれる者はいないが、観察する項目によっては両者に含まれるものが存在してもかまわない。(e.g. 1966年および1967年の乳児死亡率)
率(rate): 比の特殊な形で、分母が時間になったものを言う。したがって、事象が発生する速さを示す指標である。たとえば、罹患率、死亡率などは率である。
率=a/b
Aは事象の発生数(死亡率の観察においては死亡者数)、bは観察時間の合計であり、次元(ディメンジョン)は時間の-1乗(1/時間)である。
引用: 中村好一. 基礎から学ぶ楽しい疫学 第4版, p18-p21
[内容]
2つのグループの比較


死亡割合(mortality propotion)は以下のように算出されている。
あかりすグループ: 5匹全員が死亡しているから、
あかりすグループの死亡割合=5りす/5りす=1(100%)
しまりすグループ: 5匹全員が死亡しているから、
しまりすグループの死亡割合=5りす/5りす=1(100%)
死亡率(mortality rate)は以下のように算出されている。
あかりすグループ:
上から、[1.0, 1.5, 0.5, 2.0, 1.0]年となっており、これらの合計は6年となり、これがこのグループの合計観察期間となる。rateはa/bで算出され、この場合のaは死亡数5りす、bは観察期間の合計6年となることから、5÷6=0.833となり、100りす年あたり約83.3年となる。
しまりすグループ:
上から、[2.0, 3.0, 4.0, 1.0, 2.0]年となっており、これらの合計は12年となり、これがこのグループの合計観察期間となる。rateはa/bで算出され、この場合のaは死亡数5りす、bは観察期間の合計12年となることから、5÷12=0.417となり、100りす年あたり約41.7年となる。
平均生存期間は以下のように算出されている。
あかりすグループ:
上から、[1.0, 1.5, 0.5, 2.0, 1.0]年となっており、これらの合計は6年となることから、5りすの平均生存期間は6÷5で1.2年となる。
しまりすグループ:
上から、[2.0, 3.0, 4.0, 1.0, 2.0]年となっており、これらの合計は12年となることから、5りすの平均生存期間は12÷5で2.4年となる。
ここで、上で算出された死亡率の逆数を求めてみる。
あかりすグループ:
1÷0.833=1.20048… 約1.2
しまりすグループ:
1÷0.417=2.39808… 約2.3
このように死亡率の逆数は平均生存期間と近似している。理由としては、以下の通りに説明されている。
死亡率

平均生存期間

全員が亡くなるまで観察できたら、合計観察期間と合計生存期間は同じになるため。
「打ち切り」が存在する場合はどうするのか?

この場合、すべてのりすの死亡について観察することができなかった(しまりすが転居したため、生死不明だったり、みけりすが調査終了時も生存していた)。そのため、全体の数を使う割合(propotion)を算出することはできないが、率(rate)については算出することができる。
上から、[4.0, 2.5, 5.0, 3.0, 2.0]年となっており、これらの合計は16.5年となり、これがこのグループの合計観察期間となる。rateはa/bで算出され、この場合のaは死亡数3りす、bは観察期間の合計16.5年となることから、3÷16.5=0.182となり、100りす年あたり約18.2年となる。平均生存期間は近似的にこの逆数になるため、1÷0.182で約5.5年が平均生存期間となる。
死亡割合と死亡率の適切な使い方として、治療効果を測定する際の例として以下の通りに整理されていた。
| イベントについて | 重要性 | 例 | |
| 死亡割合 | 一定期間中にイベントが起きるかどうか | 重要 | 妊娠22週までに流産が起きるかどうか |
| 一定期間中にイベントが起きる時期 | |||
| 死亡率 | 一定期間中にイベントが起きるかどうか | ||
| 一定期間中にイベントが起きる時期 | 重要 | 1年度に起きるはずだった死亡を、治療により4年後に延ばせれば意義はある |
11月 – 前向き研究ってなにが前向きなの? –
[前提]
コホート研究(Cohort study): 調査時点である要因をもつ集団(暴露群)ともたない集団(非暴露群)を追跡し、両郡の疾病の罹患率または死亡率を比較する方法である。
前向きコホート研究(prospective cohort study): 現在から将来にわたって観察する研究。

オッズ比(odds ratio): オッズとは、「見込み」のことで、ある事象が起きる確率pの、その事象が起きない確率(1-p)に対する比を意味する。
| 罹患あり | 罹患なし | |
| 暴露群 | A | B |
| 非暴露群 | C | D |
例えば、暴露郡における罹患オッズは、「A:B」となる。
ここで、暴露群と非暴露群の「罹患あり」の比を比較し、暴露が相対的に罹患にどのくらい影響を及ぼすのか調べる場合は、以下の式に基づいて算出される。

これは、暴露群と非暴露群それぞれのグループにおける暴露郡と非暴露群における罹患オッズの比を求めている。
引用: 日本疫学会. はじめて学ぶやさしい疫学, p23-25, p62
[内容]
病気の原因を調べるときには、「いま病気になっている」ことよりも「新たに病気になる」ことを調べることがたいせつ。
いま病気になっている: 有病(prevalence)
- 現在病気であるという状態に注目
- ある時点ですでに病気をもっていること
新たに病気になる: 発生(incidence)
- 病気の発生、死亡などの健康に関連するイベントが起きた時点に注目
- 発症、または罹患
- 前向きコホート研究の例
(たばこと心疾患の関係を調査する)
対象者の前提条件: 現在心疾患にかかっていない人で将来心疾患を発生する可能性のある人を対象。
グループ分け: 喫煙グループ, 非喫煙グループ
何を調べたいのか: 2つのグループの心疾患リスクの差がどれだけあるのか
対象群:
| 心疾患発生あり | 心疾患発生なし | |
| 喫煙者 | 70 | 760 |
| 非喫煙者 | 30 | 1140 |
喫煙者の合計: 830人, 非喫煙者の合計: 1170人
上の表をもとに、リスク(発生割合)を計算したのが下記の表となる。
| 心疾患発生あり | 心疾患発生なし | |
| 喫煙者 | 70/830→8.4% | 760/830→91.6% |
| 非喫煙者 | 30/1170→2.6% | 1140/1170→97.4% |
*各計算では、小数点第3位を四捨五入して100をかけている。
喫煙グループと非喫煙グループの心疾患発生のリスク差: リスクの絶対量の違いを測る
8.4%ー2.6%=5.9%(前段の四捨五入の処理の関係上、5.8ではなく5.9となる)
このことから、喫煙グループと非喫煙グループがそれぞれ100名いたとすると、喫煙グループに心疾患の人が6名くらい多くいるということになる。
喫煙グループと非喫煙グループの心疾患発生のリスク比: リスクの相対的な違いを測る
8.4%÷2.6%=3.3(前段の四捨五入の処理の関係上、3.2ではなく3.3となる)
このことから、喫煙グループは非喫煙グループに比べ、心疾患発生リスクが3.3倍多いということになる。
喫煙グループと非喫煙グループの間で心疾患発生に違いがあるかオッズ比を求める

このことから、喫煙の暴露によって心疾患リスクが3.5倍に上昇するということがいえる。
12月 – みんなオッズ比を計算すればいいじゃないの –
[前提]
コホート研究(Cohort study): 調査時点である要因をもつ集団(暴露群)ともたない集団(非暴露群)を追跡し、両郡の疾病の罹患率または死亡率を比較する方法である。
後向きコホート研究(retrospective cohort study): 過去の一時点における記録や資料をもとに現在にわたって観察する研究。

| 症例群 (ケース) | 対照群 (コントロール) | |
| 暴露群 | a | b |
| 非暴露群 | c | d |
症例対照研究(case-control study)では、ある疾病に罹患した者(症例)と、罹患していない者から抽出した対照のそれぞれにおける過去の暴露状況を比較する。したがって、症例対照研究においては、対照群は必ずしも母集団の非罹患群を代表しておらず、母集団の罹患率の推定は難しい。そのため、相対危険と寄与危険は算出不可能であり、オッズ比を相対寄与の近似値として用いる。

引用: 日本疫学会. はじめて学ぶやさしい疫学, p25
[内容]
「後ろ向き研究」の説明
前向き研究と後ろ向き研究も同じことを調べており、後ろ向き研究の中の症例対照研究では、症例群と対照群の数のバランスを取るために、コントロールをランダムに抽出するということも可能である。
ただし、症例対照研究では、コントロールは母集団を代表していないので、グループ別でオッズ比を求めることはできない。以下は例示された表をもとに算出を行なっていく。
| 心疾患あり (ケース) | 心疾患なし (コントロール) | |
| 喫煙あり(暴露群) | 70 | 40 |
| 喫煙なし(非暴露群) | 30 | 60 |

この結果は、前向き研究のオッズ比と同じになっており、表の横向きで計算するオッズ比と喫煙の有無から表のたて向きに計算するオッズ比は必ず等しくなる。
このことから、後ろ向き研究においてもオッズ比は計算できるとされていた。
- すべての研究でオッズ比は使えるのか
イベントの発生頻度が小さいほど、リスク比とオッズ比はよく似た値になるが、イベント頻度が大きいほどこれらに乖離がみられるため、いつもオッズ比を使えばよいということではなく、前向き研究ではリスク差やリスク比を報告しなければならないとされている。
- ケース・コントロール研究の注意点
- 例えば、喫煙と心疾患との関係を調査するときは、調査時点の喫煙状況を調査するのではなく、過去に遡って喫煙状況を調べる必要がある。
- 前向き研究よりも、ケース・コントロール研究では「バイアス」が入らないように工夫する必要がある。
情報バイアス・・・過去の暴露情報は記憶や記録に頼るため、暴露情報の信頼性はコホート研究に比べ劣る。
選択バイアス・・・研究対象者(症例と対照)の選択に偏りがある可能性がある(選択バイアス)。
復習ノート
(10月)
死亡率と死亡割合の使い分けについては、以下の指標を参考にする。
死亡割合が適切な指標
- 一定期間中にイベントが起きるかどうかが重要な場合
- 一定期間中にイベントが起きる時期が重要ではない場合
死亡率が適切な指標
- 一定期間中にイベントが起きるかどうかが重要ではない場合
- 一定期間中にイベントが起きる時期が重要な場合
(11月)
前向きコホート研究(prospective cohort study): 現在から将来にわたって観察する研究。

前向きコホート研究の場合で、
| 罹患あり | 罹患なし | |
| 暴露群 | A | B |
| 非暴露群 | C | D |
とすると、オッズ比は以下のように算出される。

(12月)
前向きコホート研究(prospective cohort study): 現在から将来にわたって観察する研究。
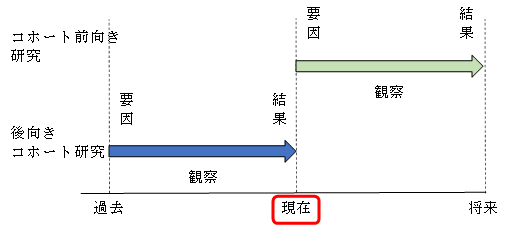
後向きコホート研究(retrospective cohort study): 過去の一時点における記録や資料をもとに現在にわたって観察する研究。
後ろ向きコホート研究の場合で、
| 症例群 (ケース) | 対照群 (コントロール) | |
| 暴露群 | a | b |
| 非暴露群 | c | d |
とすると、オッズ比は以下のように算出される。

- すべての研究でオッズ比は使えるのか
イベントの発生頻度が小さいほど、リスク比とオッズ比はよく似た値になるが、イベント頻度が大きいほどこれらに乖離がみられるため、いつもオッズ比を使えばよいということではなく、前向き研究ではリスク差やリスク比を報告しなければならないとされている。
- ケース・コントロール研究の注意点
- 例えば、喫煙と心疾患との関係を調査するときは、調査時点の喫煙状況を調査するのではなく、過去に遡って喫煙状況を調べる必要がある。
- 前向き研究よりも、ケース・コントロール研究では「バイアス」が入らないように工夫する必要がある。
情報バイアス・・・過去の暴露情報は記憶や記録に頼るため、暴露情報の信頼性はコホート研究に比べ劣る。
選択バイアス・・・研究対象者(症例と対照)の選択に偏りがある可能性がある(選択バイアス)。